積分表大全高等數(shù)學(xué)
在高等數(shù)學(xué)中,積分表是解決積分問題的重要工具。我們可以看到有多個資源提供了積分公式的大全,包括但不限于以下幾種類型的積分:
1. 含有 \(ax + b\) 的積分
2. 含有 \(\sqrt{ax + b}\) 的積分
3. 含有 \(x^2 \pm a\) 的積分
4. 含有 \(ax^2 + b\) 的積分
5. 含有 \(ax^2 + bx + c\) 的積分
6. 含有 \(\sqrt{x^2 + a^2}\) (\(a > 0\))的積分
7. 含有 \(\sqrt{x^2 - a^2}\) (\(a > 0\))的積分
8. 含有 \(\sqrt{a^2 - x^2}\) (\(a > 0\))的積分
9. 含有 \(\sqrt{\pm ax^2 + bx + c}\) (\(a > 0\))的積分
10. 含有 \(\sqrt{\pm \frac{x-a}{x+a}}\) 或者 \(\sqrt{(x-a)(b-x)}\) 的積分
11. 含有三角函數(shù)的積分
12. 含有反三角函數(shù)的積分(其中 \(a > 0\))
13. 含有指數(shù)函數(shù)的積分
14. 含有對數(shù)函數(shù)的積分
15. 含有雙曲函數(shù)的積分
這些積分公式通常在高等數(shù)學(xué)的教科書附錄中可以找到,也可以在專門的數(shù)學(xué)資源網(wǎng)站上查詢到。例如,科學(xué)空間 BoJone 提供了一個電子版本的積分公式表,其中數(shù)學(xué)公式采用 MathJax 技術(shù)顯示,方便讀者查閱 。百度文庫上也有一個完整的高等數(shù)學(xué)積分公式表,包含了常用的積分公式 。
如果你需要具體的積分公式或者對某個特定類型的積分有疑問,可以提供更詳細(xì)的信息,我可以進(jìn)一步幫助你。
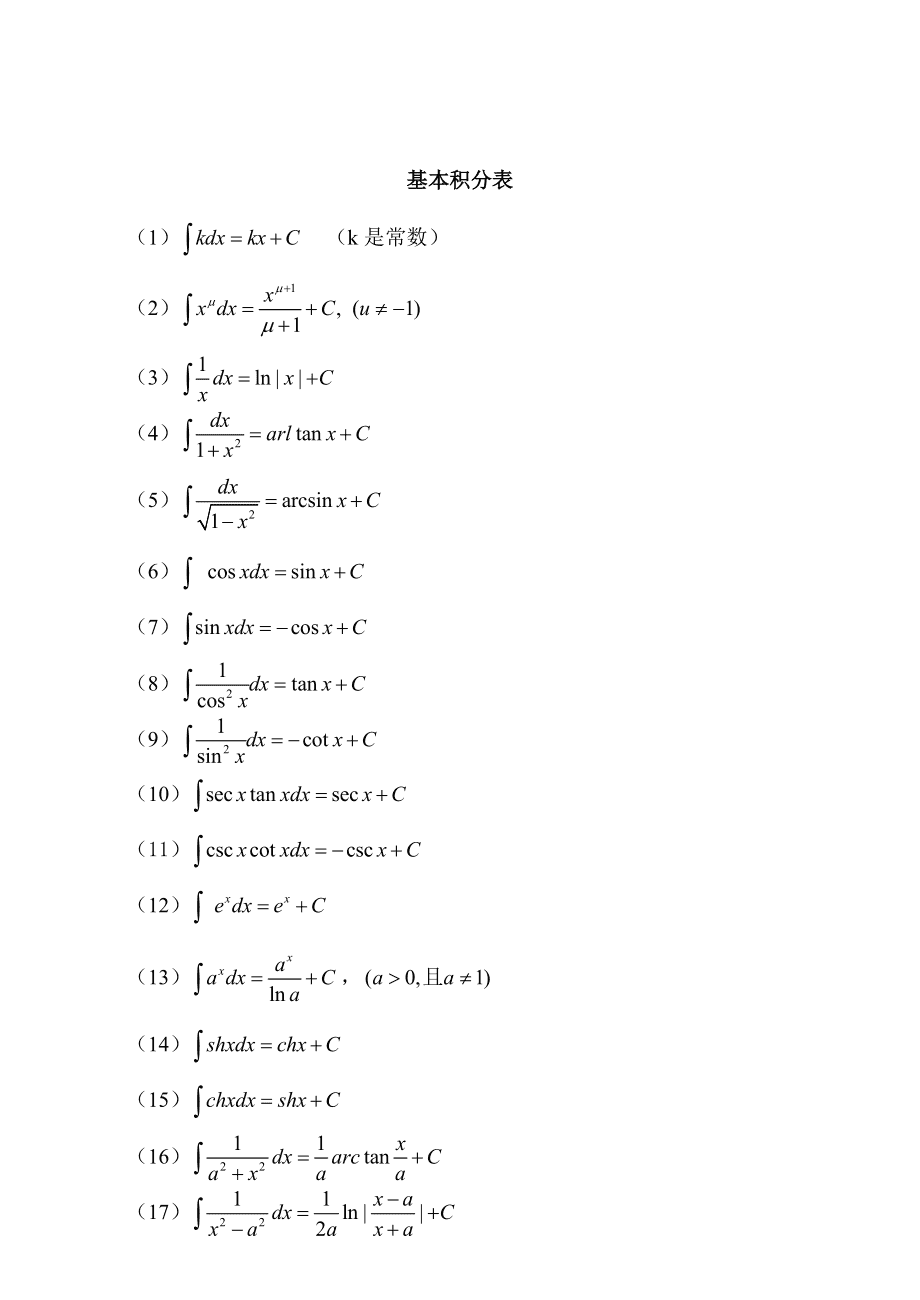
基本積分表大全
基本積分表包含了多種類型的積分公式,這些公式在解決積分問題時非常有用。以下是一些常見的積分公式:
1. 對于形如 \(\int x^n dx\) 的積分,如果 \(n \neq -1\),則有 \(\int x^n dx = \frac{1}{n+1}x^{n+1} + C\)。
2. 對于形如 \(\int \frac{1}{x+a} dx\) 的積分,結(jié)果是 \(\ln|x+a| + C\)。
3. 對于形如 \(\int \frac{1}{\sqrt{a+bx}} dx\) 的積分,結(jié)果是 \(\frac{2}{\sqrt{b}} \sqrt{a+bx} + C\)。
4. 對于三角函數(shù)的積分,例如 \(\int \sin x dx = -\cos x + C\) 和 \(\int \cos x dx = \sin x + C\)。
5. 對于指數(shù)函數(shù)的積分,例如 \(\int e^x dx = e^x + C\)。
6. 對于對數(shù)函數(shù)的積分,例如 \(\int \frac{1}{x} dx = \ln|x| + C\)。
7. 反三角函數(shù)的積分,例如 \(\int \frac{1}{\sqrt{a^2-x^2}} dx = \arcsin\left(\frac{x}{a}\right) + C\)。
8. 雙曲函數(shù)的積分,例如 \(\int \sinh x dx = \cosh x + C\) 和 \(\int \cosh x dx = \sinh x + C\)。
這些公式只是積分表中的一小部分,完整的積分表會包含更多復(fù)雜的函數(shù)和積分技巧。如果你需要更詳細(xì)的積分表,可以參考相關(guān)的數(shù)學(xué)教材或者在線資源,例如百度文庫中的《高等數(shù)學(xué)積分表大全》,或者新東方在線提供的高等數(shù)學(xué)公式手冊。這些資源通常會提供更全面的積分公式列表,以及一些特殊函數(shù)的積分方法。
高數(shù)不定積分24個基本公式
不定積分是高等數(shù)學(xué)中的一個重要概念,它與導(dǎo)數(shù)相對,用于求解原函數(shù)。以下是24個基本的不定積分公式:
1. \(\int x^n dx = \frac{1}{n+1}x^{n+1} + C\) (\(n \neq -1\))
2. \(\int \frac{1}{x} dx = \ln|x| + C\)
3. \(\int e^x dx = e^x + C\)
4. \(\int a^x dx = \frac{1}{\ln a}a^x + C\) (\(a > 0, a \neq 1\))
5. \(\int \sin x dx = -\cos x + C\)
6. \(\int \cos x dx = \sin x + C\)
7. \(\int \tan x dx = -\ln|\cos x| + C\)
8. \(\int \cot x dx = \ln|\sin x| + C\)
9. \(\int \sec x dx = \ln|\sec x + \tan x| + C\)
10. \(\int \csc x dx = -\ln|\csc x + \cot x| + C\)
11. \(\int \frac{1}{1+x^2} dx = \arctan x + C\)
12. \(\int \frac{1}{\sqrt{1-x^2}} dx = \arcsin x + C\)
13. \(\int \frac{1}{x\sqrt{x^2-1}} dx = \frac{1}{2}\ln\left|\frac{x+\sqrt{x^2-1}}{x-\sqrt{x^2-1}}\right| + C\)
14. \(\int \frac{1}{x^2-a^2} dx = \frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right| + C\)
15. \(\int \frac{1}{x^2+a^2} dx = \frac{1}{a}\arctan\left(\frac{x}{a}\right) + C\)
16. \(\int \frac{1}{x^2+a^2+1} dx = \frac{1}{a}\arctan\left(\frac{x}{a}\right) + C\)
17. \(\int \frac{1}{\sqrt{x^2+a^2}} dx = \ln|x+\sqrt{x^2+a^2}| + C\)
18. \(\int \frac{1}{\sqrt{x^2-a^2}} dx = \ln|x+\sqrt{x^2-a^2}| + C\)
19. \(\int e^{ax} \cos bx dx = \frac{e^{ax}\sin bx}{a^2+b^2} + C\)
20. \(\int e^{ax} \sin bx dx = \frac{e^{ax}\cos bx}{a^2+b^2} - \frac{b}{a^2+b^2}e^{ax}\sin bx + C\)
21. \(\int \sin ax \cos bx dx = -\frac{\sin(a+b)x}{(a+b)^2} + \frac{\sin(a-b)x}{(a-b)^2} + C\)
22. \(\int \cos ax \cos bx dx = \frac{\sin(a+b)x}{(a+b)^2} + \frac{\sin(a-b)x}{(a-b)^2} + C\)
23. \(\int \sin ax \sin bx dx = -\frac{\cos(a+b)x}{2(a+b)^2} + \frac{\cos(a-b)x}{2(a-b)^2} + C\)
24. \(\int \cos ax \sin bx dx = \frac{\sin(a+b)x}{2(a+b)^2} - \frac{\sin(a-b)x}{2(a-b)^2} + C\)
其中 \(C\) 是積分常數(shù),表示積分的不確定性。這些公式在解決不定積分問題時非常有用。

 微信掃一掃打賞
微信掃一掃打賞