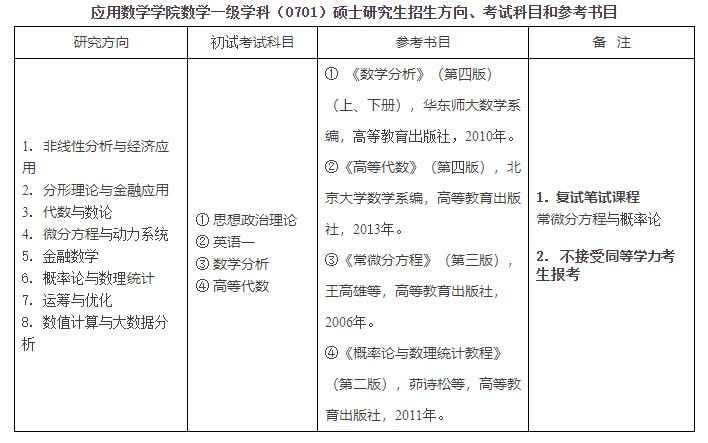
應用數(shù)學考研科目
應用數(shù)學考研科目一般包括以下幾個方面:
1. 政治理論:這是所有考研科目的必考科目,主要考察學生對基本政治理論的掌握和理解。
2. 外國語:通常為英語,部分學校可能也提供其他語言的選擇。主要考察學生的外語閱讀、寫作和翻譯能力。
3. 數(shù)學分析:這是數(shù)學專業(yè)的核心課程之一,主要涉及實數(shù)、函數(shù)、極限、連續(xù)性、微分、積分等基本數(shù)學概念和理論。
4. 高等代數(shù):同樣是數(shù)學專業(yè)的核心課程,主要內(nèi)容包括線性代數(shù)、群論、環(huán)論、域論等。
5. 概率論與數(shù)理統(tǒng)計:涉及隨機事件的概率、隨機變量及其分布、大數(shù)定律、中心極限定理、統(tǒng)計推斷等內(nèi)容。
6. 常微分方程:研究微分方程的解法和性質(zhì),包括線性微分方程、非線性微分方程、偏微分方程等。
7. 復變函數(shù):主要研究復數(shù)域上的函數(shù)的性質(zhì)和應用,包括解析函數(shù)、復變函數(shù)的積分和級數(shù)等。
8. 數(shù)值分析:涉及數(shù)值方法在數(shù)學問題中的應用,如數(shù)值積分、數(shù)值微分、數(shù)值代數(shù)等。
9. 實變函數(shù)與泛函分析:研究實數(shù)域上的函數(shù)和泛函的性質(zhì),包括勒貝格積分、測度論、巴拿赫空間等。
10. 偏微分方程:研究偏微分方程的解法和性質(zhì),如橢圓型、雙曲型和拋物型偏微分方程。
11. 組合數(shù)學:涉及組合計數(shù)、圖論、組合優(yōu)化等。
12. 最優(yōu)化理論:研究如何找到最優(yōu)解的方法,包括線性規(guī)劃、非線性規(guī)劃、整數(shù)規(guī)劃等。
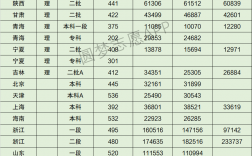
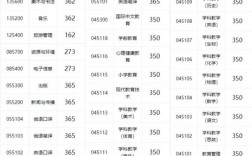
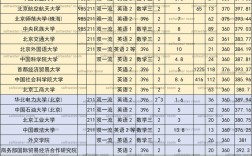
具體的考試科目和內(nèi)容可能會建議查看目標學校的考研招生簡章或咨詢相關(guān)教育部門獲取詳細信息。

 微信掃一掃打賞
微信掃一掃打賞